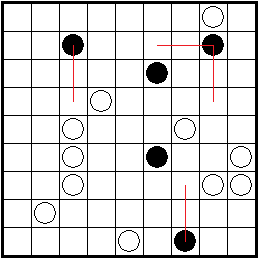
Yet Another Logic Puzzle Blog: Pearls of Wisdom Tips

1. Draw a single loop that connects the centers of the grid cells.

2. The loop may only travel horizontally or vertically, not diagonally (so all turns are right angles).

3. The loop may only turn at the centers of the grid cells.

4. The loop may not cross itself or branch off.
5. The loop must pass through every pearl (circle) on the grid.
6. The loop may not turn at a white pearl, but must turn at at least one of the adjacent cells in the loop.
7. The loop must turn at a black pearl, but may not turn at both of the adjacent cells in the loop.

Make sure you read the loop tips.

So, first: remember that if the loop goes into a white pearl, it automatically will just go straight through. And, if a line goes out of a black pearl, it will always go out two. Just keep those rules in mind.

Also keep in mind that if a straight line goes into a white pearl (see the next example for an illustration), it must turn afterwards. If it can't turn one way, then the other way is the way it goes.

I personally rarely use x's on this puzzle, but it might be useful. I'll phrase things with x's here and use them sometimes, even though I don't use them. The best place to use them is where they aren't obvious like this:

This line going out the top needs to turn because of rule 6, so it can't go up:

Theorem 1: A white pearl next to an x must have a line going through the pearl perpendicular to the x.

This means that:

implies

and

implies

There are other situations, but you get the idea.

A special case is two white pearls next to a wall:

They need to go through like normal, but also turn up because they have to turn on one side of them (and the other side is straight because it's another white pearl):

Theorem 2: If three or more white cells are next to each other, parallel lines must be drawn in all of the white cells.

This means that if there's this:

There must be this:

If there's more than three, it's just the same thing in all of them. To see why it's true, just try making it one line going through them all. The middle pearl won't turn on either side.

Theorem 3: If a line goes up to a white pearl straight-on when another white pearl is behind it, the line must turn.

This one is kind of confusing. Here's an example:

There is an x here because of this theorem:

If the line went through that way, it would have kept on going straight, making that white pearl on the right not have any lines turning outside it.

You can actually use Theorem 1 now a couple times to figure this all out too:

Theorem 4: If there's a line coming up to a white pearl on both sides straight-on, the line going through the white pearl must be perpendicular to the lines.

Theorems 2, 3, and 4 are all really similar, deriving from Rule 6. They're just stating less obvious things.

Anyway, example:

We need to do this, for the same reasons as the last two theorems:

Theorem 5: If there is an x next to a black cell or one away from it, a line must be drawn opposite the x.

Here's a bunch of examples:

implies

That should be enough examples.

Theorem 6: If two black pearls are next to each other, there is an x between them.

This won't fit in anything smaller than a 6x6 grid, and is really simple, so I won't give any examples. Just remember that both black pearls will then extend because of Theorem 5.

Theorem 7: If a line goes into a cell next to a black pearl that is NOT straight-on, there is an x between the cell and the black pearl.

Example:

The black pearl can't go right, because it won't go out two. This Theorem says this x goes here (and makes this line by Theorem 5):

There are a few other random things that aren't really theorems as well, so I'll solve the example puzzle above.

First I'll use Theorem 5 on these black pearls:

I can now use Theorem 7 on this one:

I can use Theorem 1 on all of these white pearls on the side:

I can also use Theorem 2 on these:

The black pearl on the bottom right can't go right, because then it has nowhere to go. It must go left:

Theorem 1 on this white cell:

There can't be any closed loops, so this line goes here:

I just realized I didn't use Theorem 7 fully earlier, I can do this too:

By rule six, this line must turn:

This line extends this way:

This one also can extend now, going through this white pearl and going further:

By Theorem 7:

Now these lines must extend this way:

Now Theorem 7 again:

This loop on the top right can't touch itself, and all of this happens as a result:

I'll have to admit, even though this is my puzzle I got stuck for a bit and got a bit worried there wasn't a solution and I messed up when I made it. But, remember Theorem 5 of the Loop Tips? The one about an even number of lines going into a closed area? Think about the rectangle from R7C4 to R8C5. That's a closed area, and if the line in R8C4 goes right or up, there's an odd number of lines going into the area. That line must go left:

Now these lines extend:

Think of R6C2 and R7C2. Both of them need to turn, because they're coming out of a white pearl and the other side went straight. They can't turn into each other, because then there's a closed loop. They both must turn the other way: